MATEMÁTICAS BLOQUE 3
REPASO DEL BLOQUE
El uso de técnicas de estudio para mejorar el desempeño en la escuela o en la universidad es algo común entre los jóvenes y adolescentes que desean superarse de forma permanente. Unas de las técnicas más conocidas, pero menos comprendidas, es la del repaso. El repaso consiste en la relectura o revisión de material leído previamente a fines de asentarlo en la memoria de largo plazo. El método que utilicemos para efectuar este repaso determinará directamente la eficacia con la que, posteriormente, lograremos recuperar el material almacenado.
SUMAS Y RESTAS DE FRACCIONES CON DIFERENTE DENOMINADOR
Hay que calcular las fracciones equivalentes. Para cada fracción haremos lo siguiente.
- Sustituimos su denominador por el denominador común.
- Calculamos su numerador de la siguiente manera: dividimos el denominador común por el denominador original de cada fracción. El resultado obtenido lo multiplicamos por el numerador original, obteniendo el numerador de la fracción equivalente.
Tranquilo, es más fácil de lo parece. Lo entenderás perfectamente con este ejemplo:
Vamos a hacerlo paso a paso:
1.- Primero calculamos el denominador común: 4 x 3 x 5 = 60
Ahora vamos a calcular el numerador equivalente de cada fracción:
Primera fracción:
Dividimos el denominador común entre su denominador: 60 : 4 =15
Multiplicamos este resultado por su numerador: 15 x 2 = 30
Segunda fracción:
Dividimos el denominador común entre su denominador: 60 : 3 = 20
Multiplicamos este resultado por su numerador: 20 x 6 = 120
Tercera fracción:
Dividimos el denominador común entre su denominador: 60 : 5 =12
Multiplicamos este resultado por su numerador: 12 x 3 = 36
Ya podemos sustituir las fracciones originales por sus fracciones equivalentes:
Para terminar, procedemos a la suma:
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4
UBICACIÓN DE UN OBJETO EN EL ESPACIO
La ubicación en el espacio es un concepto que nos sirve para aprender si las cosas están arriba, abajo, a la derecha, a la izquierda. Reconocer estas ubicaciones nos ayudará en muchas cosas de la vida diaria como por ejemplo si estamos arriba o debajo del tobogán, o si escribimos con la mano derecha o izquierda.
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5
EJERCICIO 1 EJERCICIO 2
CÁLCULOS DE POLÍGONOS PERÍMETRO: es la suma de las longitudes de todos los lados del polígono.
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4
PERÍMETRO DE POLÍGONOS
Un polígono está formado por una línea poligonal cerrada y la superficie interior.
Todos sus lados tienen que ser líneas rectas.
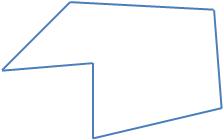
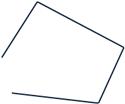
Veamos ahora 2 figuras que no son polígonos:
Porque son líneas abiertas o porque alguno de sus lados no es una línea recta.
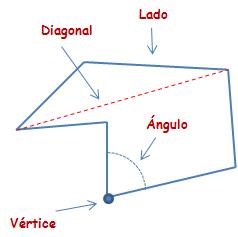
En un polígono se pueden distinguir:
- Lados
- Vértices
- Ángulos
- Diagonales (líneas rectas que unen dos vértices no consecutivos)
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4
MULTIPLICACIÓN Y DIVISIÓN COMO OPERACIONES INVERSAS
En las inversas, conociendo el resultado de la operación directa correspondiende, se puede hallar el otro resultado. La sustracción es inversa a la adición, la división a la multiplicación, entre otras
Ejemplo.
a).- Para la resta o substracción, si conozco un sumando y el total de una suma 25 + a = 72, puedo obtener el resultado con la resta o sustracción 72 (minuendo) – 25(sustraendo) = 47(resta, exceso o diferencia): 72 – 25 = 47
b).- Para la división si conozco un factor y el producto de la multiplicación a x 4 = 32 puedo encontrar el resultado con la división 32 (dividendo) entre 4 (divisor) = 8 (cociente): 32 ÷ 4 = 8;
VÍDEO 1 VÍDEO 2 VÍDEO 3
EJERCICIO 1 EJERCICIO 2
MULTIPLOS Y SUBMULTIPLOS DE UNIDADES DE MEDIDA
Medir es un concepto fácil de aprender si dentro de las actividades del niño se complementan con herramientas básicas y demostraciones que le ayudaran a realizar pequeñas medidas, las demostraciones en el aula pueden estar basadas a las medidas del pizarrón, la estatura de los compañeros del aula, la estatura del maestro o bien las medidas de un cuaderno. El método más efectivo es realizar juegos de medidas y demostraciones con regletas o cintas métricas dentro del aula o en el jardín, este método se denomina demostración de unidades de medida y es un trabajo práctico.
 VÍDEO 1 VÍDEO 2 VÍDEO 3
VÍDEO 1 VÍDEO 2 VÍDEO 3
Unidad de medida principal: El metro
Los pequeños podrán aprender en esta etapa la unidad de medida principal y otras de menor complejidad, como la masa y algo de volumen repasaremos algunas de menor complejidad y la forma de enseñarlas bajo el método de las demostraciones en una práctico o juegos sencillos
El metro es la principal medida de longitud, el mismo está dividido de la siguiente manera (siendo sus submúltiplos):
- Decimetros = dm
- Centímetros = cm
- Milímetros = mm
El metro también tiene grandes múltiplos como lo son:
- Kilómetro = Km
- Hectómetro = hm
- Decámetro = dam
¿Para que se usa el metro?
Los niños pueden medir con una cinta métrica o un metro el largo, el ancho y la altura de los objeto y personas. En otras palabras, una demostración será realizada por los niños para medir longitudes. También pude medir algunas longitudes con una regleta o regla escolar.
Más tarde con la ayuda de un esquema los niños pueden aprender a hacer conversiones de una medida a otra: siguiendo un procedimiento como multiplicar o dividir cuantos ceros se hayan movido
Unidades de medida de Volumen
La unidad de medida para medir capacidad es el litro, en relación al litro también existen múltiplos y submúltiplos; encontrando la siguiente clasificación.
El litro tiene los siguientes submúltiplos de 10:
- Decilitro
- Centilitro
- Mililitro
El litro tiene grandes múltiplos como lo son:
- Kilolitro
- Hectolitro
- Decalitro
Unidades Medidas de Masa
Las unidades de masa no difieren tampoco en tener múltiplos y submúltiplos, y son aquellas que sirven para medir el peso que puede tener un objeto o alguna materia, entre ellas encontramos las siguientes medidas:
La unidad de medida para masa es el kilogramo de manera que encontramos los siguientes submúltiplos
- Hectogramo
- Decagramo
- Gramo
- Decigramo
- Centigramo
- Miligramo
Si observamos el esquema lo vemos de la siguiente manera:

EJERCICIO 1 EJERCICIO 2
CONSTRUCCIÓN DE GRÁFICA DE BARRAS
Las Gráficas y las Tablas representan e interpretan la información de diferentes fuentes, de manera clara y precisa.
Las Gráficas permiten ver la información que contiene las tablas de manera más fácil y rápida.
La Gráfica de barras es la representación Gráfica de una información en específico, como su nombre lo indica se representa por columnas representado por los valores representados.
La gráfica de barras o diagrama de columnas se puede dividir en varias secciones, por ejemplo:
- El Titulo de la gráfica (Es el nombre de la Gráfica)
- El Eje Horizontal (Valor en eje Horizontal)
- El Eje Vertical (Valor en eje Vertical)
- Las Barras o Columnas (Frecuencia del Valor Requerido)
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3




VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5
SISTEMAS DE NUMERACIÓN DECIMAL Y MAYA
¿Qué es la Numeración Decimal?
Es el sistema para expresar todos los números con cantidad limitada de palabras y de signos.
La numeración decimal es el sistema que se utiliza los diez números conocidos como Naturales:
0,1, 2, 3, 4, 5, 6, 7, 8, 9.
Recuerda…….
El cero no tiene valor por si mismo, si no únicamente valor posicional, es decir, por el lugar que ocupa.
Los números se escriben teniendo en cuenta que, cualquier cifra situada inmediatamente a la izquierda de otra significa que es diez unidades mayor que esta.
Y, a la inversa, cualquier cifra situada inmediatamente a la derecha es diez unidades menores que esta.
Para escribir un numero natural en este sistema de numeración tendremos en cuenta las siguientes reglas:
1° Cada cifra tiene dos valores, uno absoluto, representando por el signo de la misma y otro relativo, que depende del lugar en el que ocupe en la escritura del numero.
2° Toda cifra escrita a la izquierda de otra representa unidades de orden inmediato superior. Así la primera cifra representa unidades simples, la segunda cifra representa las decenas, la tercera centenas, la cuarta unidades de millar y así sucesivamente.
Sistema de Numeración Maya
Los mayas idearon un sistema de numeración como un instrumento para medir el tiempo y no para hacer cálculos matemáticos Maya, los mayas tienen que ver con los días, meses, años y con la manera en que organizaban el calendario, utilizaban un sistema de numeración vigesimal (de base 20), similar al de otras civilizaciones mesoamericanas.
Los mayas desarrollaron el concepto del cero alrededor del año 36 a.C., representándolo con una concha, idearon un sistema de base 20 con el 5 como base auxiliar.
La unidad se representaba con un punto, dos, tres y cuatro puntos servían para representar el 2, 3 y 4.
El 5 era una raya Horizontal y se le añadían los puntos necesarios para representar 6, 7, 8 y 9. Para el 10 se usaban dos rayas y de la misma forma se continúa hasta el 20 con cuatro rayas.
Para escribir un número más grande 20 se usan los mismos símbolos, pero cambian su valor dependiendo de la posición en la que se pongan.
Los números mayas se escriben de abajo hacia arriba, en el primer nivel (el de hasta abajo) se escriben las unidades del 0 al 19.
En el segundo nivel se multiplica por 20. Por esto se dice que el sistema de numeración maya es vigesimal, la posición de los números mayas se escriben de forma vertical.
En el segundo orden cada punto vale 20 unidades y cada raya vale 100 unidades.




VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3
UNA MEDIDA ENTERA ENTRE UN NATURAL
Cuando hay un reparto se busca que sea equitativo y exhaustivo, es decir que se divida en partes iguales y que no sobre nada.Cuando se reparte una cantidad entera que se posible nombrar n, entre otra también entera que se puede identificar como m, el resultado sera la fracción n/m . Así el cociente de la división n entre m se representa también mediante una fracción n/m.
EJERCICIO 1 (REALIZA DIEZ EJEMPLOS)
EJERCICIO 2 (REALIZA GUÍA Y LIBRO)
VÍDEO 3 (REALIZA LA PRUEBA 5 DIVISIONES EN 2 MIN.)


VÍDEO 3 (REALIZA LA PRUEBA 5 DIVISIONES EN 2 MIN.)
SUCESIONES DE NÚMEROS CON PROGRESIÓN GEOMÉTRICA

Esto que acabo de poner es un ejemplo de progresión geométrica.
¿No te fías de mí?
¿Que cómo sabes si es una progresión geométrica?
Quizás tendría que haber empezado explicando qué es una progresión geométrica.
No es otra cosa que una sucesión en la que cada término (excepto el primero) se obtiene multiplicando el anterior por un número o cantidad fija que llamamos razón.
Que lo de antes es una sucesión parece claro (o al menos de números), porque son números dispuestos uno a continuación de otro, pero vamos a ver si se cumple eso de que cada término se obtiene multiplicando el anterior siempre por el mismo número (la razón)…

Pues sí, cada término lo obtenemos multiplicando el que va justo antes por 2, y ocurre siempre. Luego efectivamente es una progresión geométrica y además de razón 2.
EJERCICIO 1 EJERCICIO 2
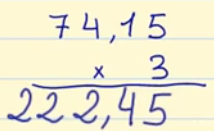
MULTIPLICACIONES DE DECIMALES POR UN NUMERO NATURAL
Para multiplicar un número decimal por un número entero, se multiplica como si el número decimal fuera un número entero.
En el resultado se separan tantas cifras decimales como tenía el número decimal.
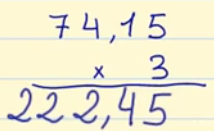
Al realizar la multiplicación de 74,15 x 3, primero multiplicamos como si no existiesen los decimales, 7415 x 3
Una vez terminada la multiplicación, contamos que 74,15 tiene dos decimales, por lo que ponemos una coma contando dos posiciones de derecha a izquierda.
Por lo tanto, el resultado será 222,45
(OJO) La coma (,) hace el papel del punto (.) decimal
EJERCICIO 1
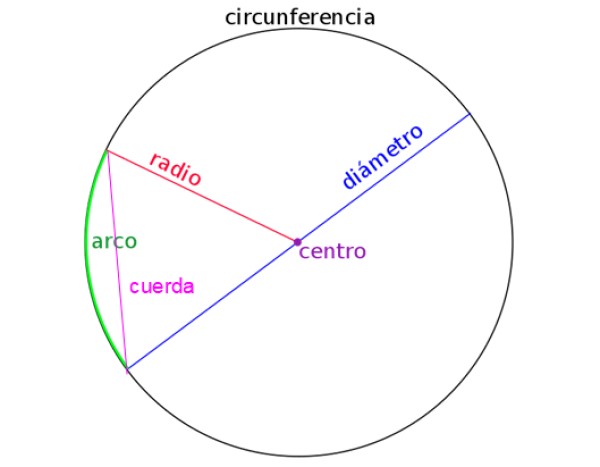
CÍRCULO Y CIRCUNFERENCIA. RADIO, DIÁMETRO Y CENTRO
Todos los puntos que estén a la misma distancia de otro punto forman una circunferencia.
• La región que queda encerrada por una circunferencia
se llama círculo.
• La cuerda es un segmento de recta que va de un punto de la
circunferencia a otro.
• El diámetro de una circunferencia es una cuerda que pasa por el centro.
• El radio solo va de un punto de la circunferencia al centro.
• La mediatriz es la recta que separa en dos partes iguales una cuerda y forma un ángulo de 90°
con ella.

EJERCICIO 1 EJERCICIO 2
SISTEMAS DE REFERENCIAS
Los sistemas de referencia se utilizan para determinar la posición de un punto u objeto en el espacio.
Por ejemplo, en el tablero de ajedrez se utilizan letras y números para indicar la posición de una pieza.
Otros sistemas de referencia son el sistema de coordenadas geográficas y el sistema de coordenadas polares. Las coordenadas geográficas determinan la ubicación de un punto mediante la latitud y la longitud.
En el sistema de coordenadas polares la localización de un punto se define por un ángulo y una distancia.
Por ejemplo, en el tablero de ajedrez se utilizan letras y números para indicar la posición de una pieza.
Otros sistemas de referencia son el sistema de coordenadas geográficas y el sistema de coordenadas polares. Las coordenadas geográficas determinan la ubicación de un punto mediante la latitud y la longitud.
En el sistema de coordenadas polares la localización de un punto se define por un ángulo y una distancia.
EJERCICIO 1
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6
AAAAAAA
VÍDEO 1 VÍDEO 2 VÍDEO 3 VÍDEO 4 VÍDEO 5 VÍDEO 6 VÍDEO 7 VÍDEO 8 VÍDEO 9
EJERCICIO 1 EJERCICIO 2 EJERCICIO 3 EJERCICIO 4 EJERCICIO 5 EJERCICIO 6






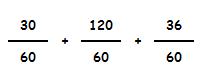
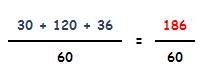







No hay comentarios:
Publicar un comentario